(Lulusan Cum Laud FPMIPA UPI )
Jendri Irawan
(Universitas Negeri Yogyakarta)
Arip Nurahman
(Universitas Pendidikan Indonesia & OpenCourseWare @ MIT, Cambridge MA. USA.)
Langkah Strategis:
1.Membangun Himpunan-himpunan Kelompok Keahlian Khusus Matematika Para Guru.
Kelompok Keahlian Khusus Matematika
Mathematics is the academic discipline, and its supporting body of knowledge, that involves the study of such concepts as quantity, structure, space and change. The mathematician Benjamin Peirce called it "the science that draws necessary conclusions".[2] Other practitioners of mathematics maintain that mathematics is the science of pattern, and that mathematicians seek out patterns whether found in numbers, space, science, computers, imaginary abstractions, or elsewhere.[3][4] Mathematicians explore such concepts, aiming to formulate new conjectures and establish their truth by rigorous deduction from appropriately chosen axioms and definitions.[5]
Through the use of abstraction and logical reasoning, mathematics evolved from counting, calculation, measurement, and the systematic study of the shapes and motions of physical objects. Knowledge and use of basic mathematics have always been an inherent and integral part of individual and group life. Refinements of the basic ideas are visible in mathematical texts originating in the ancient Egyptian, Mesopotamian, Indian, Chinese, Greek and Islamic worlds. Rigorous arguments first appeared in Greek mathematics, most notably in Euclid's Elements. The development continued in fitful bursts until the Renaissance period of the 16th century, when mathematical innovations interacted with new scientific discoveries, leading to an acceleration in research that continues to the present day.[6]
Today, mathematics is used throughout the world as an essential tool in many fields, including natural science, engineering, medicine, and the social sciences such as economics and psychology. Applied mathematics, the branch of mathematics concerned with application of mathematical knowledge to other fields, inspires and makes use of new mathematical discoveries and sometimes leads to the development of entirely new disciplines. Mathematicians also engage in pure mathematics, or mathematics for its own sake, without having any application in mind, although practical applications for what began as pure mathematics are often discovered later.[7]
Contents
- 1 Etymology
- 2 History
- 3 Inspiration, pure and applied mathematics, and aesthetics
- 4 Notation, language, and rigor
- 5 Mathematics as science
- 6 Fields of mathematics
- 7 Common misconceptions
- 8 See also
- 9 Notes
- 10 References
- 11 External links
Fields of mathematics

As noted above, the major disciplines within mathematics first arose out of the need to do calculations in commerce, to understand the relationships between numbers, to measure land, and to predict astronomical events. These four needs can be roughly related to the broad subdivision of mathematics into the study of quantity, structure, space, and change (i.e., arithmetic, algebra, geometry, and analysis). In addition to these main concerns, there are also subdivisions dedicated to exploring links from the heart of mathematics to other fields: to logic, to set theory (foundations), to the empirical mathematics of the various sciences (applied mathematics), and more recently to the rigorous study of uncertainty.
Quantity
The study of quantity starts with numbers, first the familiar natural numbers and integers ("whole numbers") and arithmetical operations on them, which are characterized in arithmetic. The deeper properties of integers are studied in number theory, whence such popular results as Fermat's Last Theorem. Number theory also holds two widely considered unsolved problems: the twin prime conjecture and Goldbach's conjecture.
As the number system is further developed, the integers are recognized as a subset of the rational numbers ("fractions"). These, in turn, are contained within the real numbers, which are used to represent continuous quantities. Real numbers are generalized to complex numbers. These are the first steps of a hierarchy of numbers that goes on to include quarternions and octonions. Consideration of the natural numbers also leads to the transfinite numbers, which formalize the concept of counting to infinity. Another area of study is size, which leads to the cardinal numbers and then to another conception of infinity: the aleph numbers, which allow meaningful comparison of the size of infinitely large sets.
Structure
Many mathematical objects, such as sets of numbers and functions, exhibit internal structure. The structural properties of these objects are investigated in the study of groups, rings, fields and other abstract systems, which are themselves such objects. This is the field of abstract algebra. An important concept here is that of vectors, generalized to vector spaces, and studied in linear algebra. The study of vectors combines three of the fundamental areas of mathematics: quantity, structure, and space. Vector calculus expands the field into a fourth fundamental area, that of change. Tensor calculus studies symmetry and the behavior of vectors under rotation. A number of ancient problems concerning Compass and straightedge constructions were finally solved using Galois theory.
Space
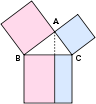
The study of space originates with geometry - in particular, Euclidean geometry. Trigonometry combines space and numbers, and encompasses the well-known Pythagorean theorem. The modern study of space generalizes these ideas to include higher-dimensional geometry, non-Euclidean geometries (which play a central role in general relativity) and topology. Quantity and space both play a role in analytic geometry, differential geometry, and algebraic geometry. Within differential geometry are the concepts of fiber bundles and calculus on manifolds. Within algebraic geometry is the description of geometric objects as solution sets of polynomial equations, combining the concepts of quantity and space, and also the study of topological groups, which combine structure and space. Lie groups are used to study space, structure, and change. Topology in all its many ramifications may have been the greatest growth area in 20th century mathematics, and includes the long-standing Poincaré conjecture and the controversial four color theorem, whose only proof, by computer, has never been verified by a human.
Change
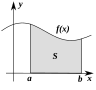
Understanding and describing change is a common theme in the natural sciences, and calculus was developed as a powerful tool to investigate it. Functions arise here, as a central concept describing a changing quantity. The rigorous study of real numbers and real-valued functions is known as real analysis, with complex analysis the equivalent field for the complex numbers. The Riemann hypothesis, one of the most fundamental open questions in mathematics, is drawn from complex analysis. Functional analysis focuses attention on (typically infinite-dimensional) spaces of functions. One of many applications of functional analysis is quantum mechanics. Many problems lead naturally to relationships between a quantity and its rate of change, and these are studied as differential equations. Many phenomena in nature can be described by dynamical systems; chaos theory makes precise the ways in which many of these systems exhibit unpredictable yet still deterministic behavior.
 |  |  |  |  |
| Calculus | Vector calculus | Differential equations | Dynamical systems | Chaos theory |
Foundations and philosophy
In order to clarify the foundations of mathematics, the fields of mathematical logic and set theory were developed, as well as category theory which is still in development. The crisis of foundations, which is the early 20th century's term for the search for proper foundations of mathematics, is a persistent phenomenon; it is illustrated by a number of controversies, including the controversy over Cantor's theory, the Brouwer-Hilbert controversy and the Bishop-Keisler controversy.
Mathematical logic is concerned with setting mathematics on a rigid axiomatic framework, and studying the results of such a framework. As such, it is home to Gödel's second incompleteness theorem, perhaps the most widely celebrated result in logic, which (informally) implies that any formal system that contains basic arithmetic, if sound (meaning that all theorems that can be proven are true), is necessarily incomplete (meaning that there are true theorems which cannot be proved in that system). Gödel showed how to construct, whatever the given collection of number-theoretical axioms, a formal statement in the logic that is a true number-theoretical fact, but which does not follow from those axioms. Therefore no formal system is a true axiomatization of full number theory. Modern logic is divided into recursion theory, model theory, and proof theory, and is closely linked to theoretical computer science.
Discrete mathematics
Discrete mathematics is the common name for the fields of mathematics most generally useful in theoretical computer science. This includes computability theory, computational complexity theory, and information theory. Computability theory examines the limitations of various theoretical models of the computer, including the most powerful known model - the Turing machine. Complexity theory is the study of tractability by computer; some problems, although theoretically solvable by computer, are so expensive in terms of time or space that solving them is likely to remain practically unfeasible, even with rapid advance of computer hardware. Finally, information theory is concerned with the amount of data that can be stored on a given medium, and hence deals with concepts such as compression and entropy.
As a relatively new field, discrete mathematics has a number of fundamental open problems. The most famous of these is the "P=NP?" problem, one of the Millennium Prize Problems.[20]
Applied mathematics
Applied mathematics considers the use of abstract mathematical tools in solving concrete problems in the sciences, business, and other areas. An important field in applied mathematics is statistics, which uses probability theory as a tool and allows the description, analysis, and prediction of phenomena where chance plays a role. Most experiments, surveys and observational studies require the informed use of statistics. (Many statisticians, however, do not consider themselves to be mathematicians, but rather part of an allied group.) Numerical analysis investigates computational methods for efficiently solving a broad range of mathematical problems that are typically too large for human numerical capacity; it includes the study of rounding errors or other sources of error in computation.






























Tidak ada komentar:
Posting Komentar